1. 前言
排序有内部排序和外部排序,内部排序是数据记录在内存中进行排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。
内部排序大致分为五种:交换排序、插入排序、选择排序、归并排序和基数排序。其中交换排序包括冒泡排序和快速排序、插入排序包括直接插入排序和希尔排序,选择排序包括简单选择排序和堆排序。
当n较大时,应采用时间复杂度为O(nlog2n)的排序方法:快速排序、堆排序或归并排序。
快速排序目前是内部排序中最好的方法,当待排序的关键字是随机分布时,快速排序的平均时间最短。
2. 自拟题目
使用冒泡排序、快速排序、直接插入排序、希尔排序、简单选择排序、堆排序、归并排序、基数排序共八种排序方法,给[8,7,4,2,1,3,5,9,0,6]按照升序和降序排序。
示例输入:
1 | [8,7,4,2,1,3,5,9,0,6] |
示例输出:
1 | [0,1,2,3,4,5,6,7,8,9] |
3. 冒泡排序
冒泡排序重复地走访过要排序的元素,依次比较相邻两个元素,如果他们的顺序错误就把他们调换过来,直到没有元素再需要交换,排序完成。这个算法的名字由来是因为越小(或越大)的元素会经由交换慢慢“浮”到数列的顶端。
以左边为水面,升序冒泡排序算法描述如下:
1、从最后一对相邻的元素开始,比较相邻的元素,如果后一个比前一个小,则调换它们的位置(小的冒泡)。
2、对每一对相邻元素作同样的工作,从最后一对到第一对。
3、第一个元素固定为最小元素,不参与接下来的比较。
4、对越来越少的元素(除了固定元素)重复上面的步骤,直到没有任何一对元素需要比较。

1 | // 冒泡排序 |
4. 快速排序
快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序,它是对冒泡排序的改进。它采用了一种分治的策略,通常称其为分治法(Divide-and-ConquerMethod)。MoreWindows同学把它归结为:挖坑填数+分治法。
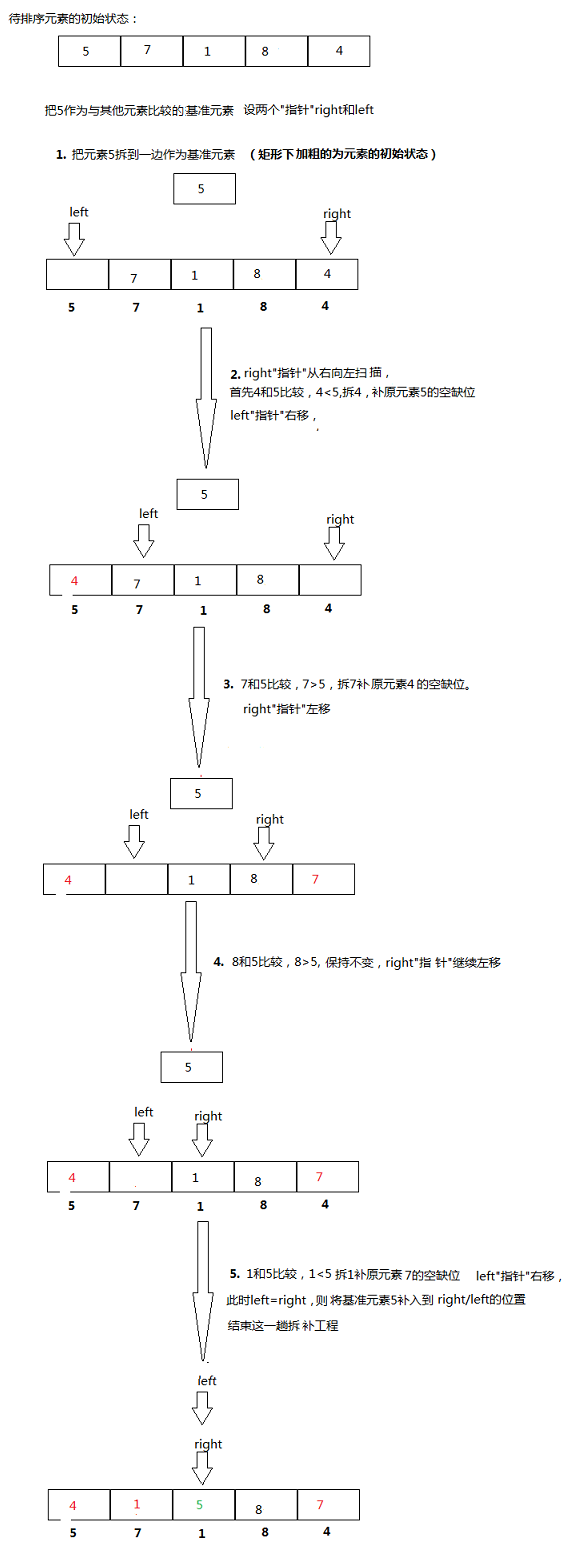
升序快速排序算法描述如下:
1、i = L; j = R; 将基准数挖出形成第一个坑a[i]。
2、j–由后向前找比基准输小的数,找到后挖出此数填前一个坑a[i]中。
3、i++由前向后找比基准数大的数,找到后也挖出此数填到前一个坑a[j]中。
4、重复执行2,3步,直到i==j,将基准数填入a[i]中。
5、以上,得到两个区,左边的区比基数小,右边的区比基数大。
6、对于得到的两个区,分别重复1-4。
1 | // 快速排序 |
5. 直接插入排序
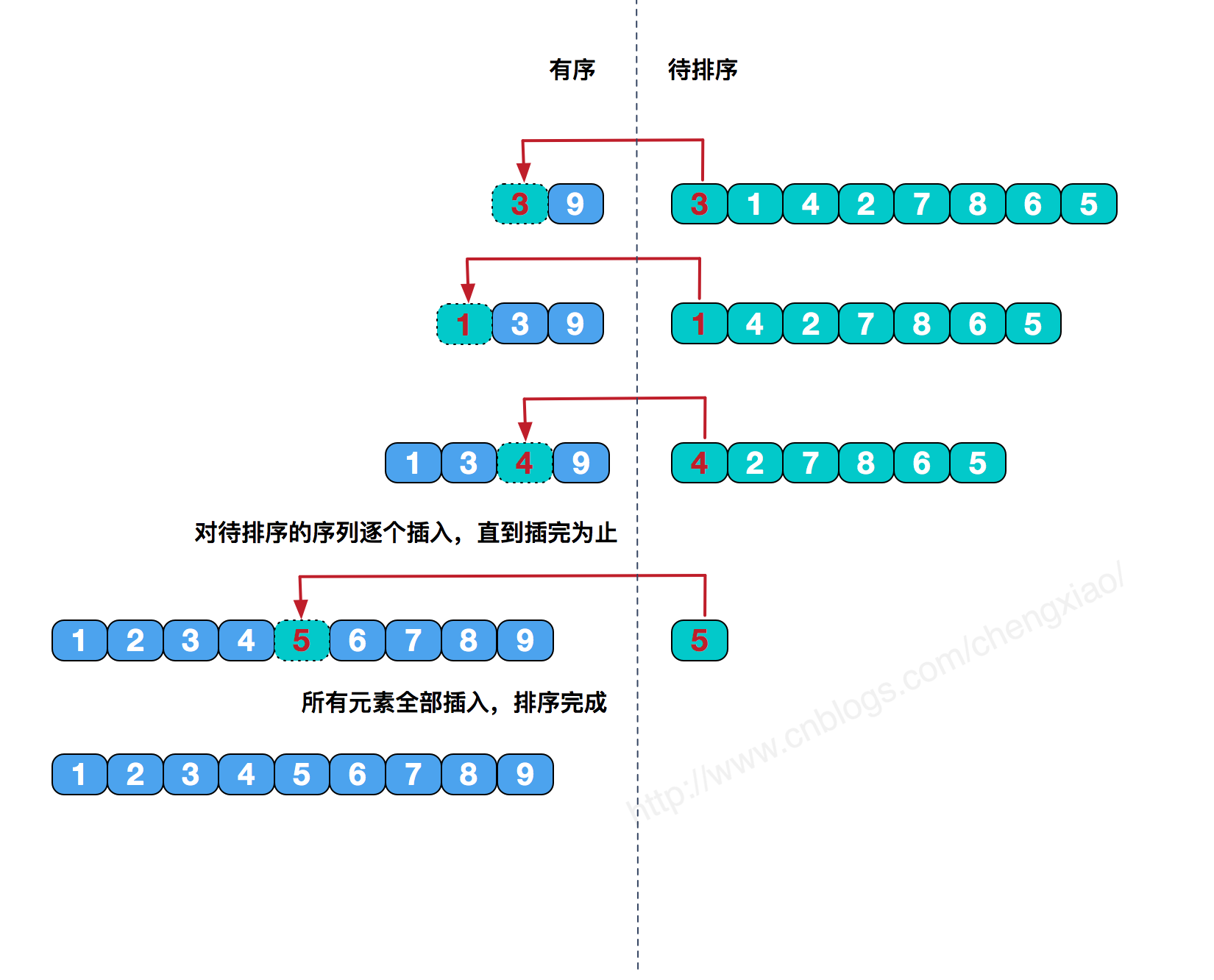
插入排序是一种简单直观的排序算法,它的工作原理非常类似于我们抓扑克牌。
升序插入算法描述如下:
1、从第一个元素开始,该元素可以认为已经被排序。
2、取出下一个元素,在已排序的元素序列中从后向前扫描。
3、如果新元素小于已排序的元素(老元素),将老元素移到下一位置。
4、重复步骤3,直到找到新元素大于或等于老元素的位置,将新元素插入到该位置。
5、重复步骤2~4。
1 | // 直接插入排序 |
6. 希尔排序
希尔排序,也叫递减增量排序,是插入排序的一种更高效的改进版本。希尔排序是不稳定的排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序,算法的最后一步就是普通的插入排序,但是到了这步,需排序的数据几乎是已排好的了(此时插入排序较快)。
假设有一个很小的数据在一个已按升序排好序的数组的末端。如果用复杂度为O(n^2)的排序(冒泡排序或直接插入排序),可能会进行n次的比较和交换才能将该数据移至正确位置。而希尔排序会用较大的步长移动数据,所以小数据只需进行少数比较和交换即可到正确位置。
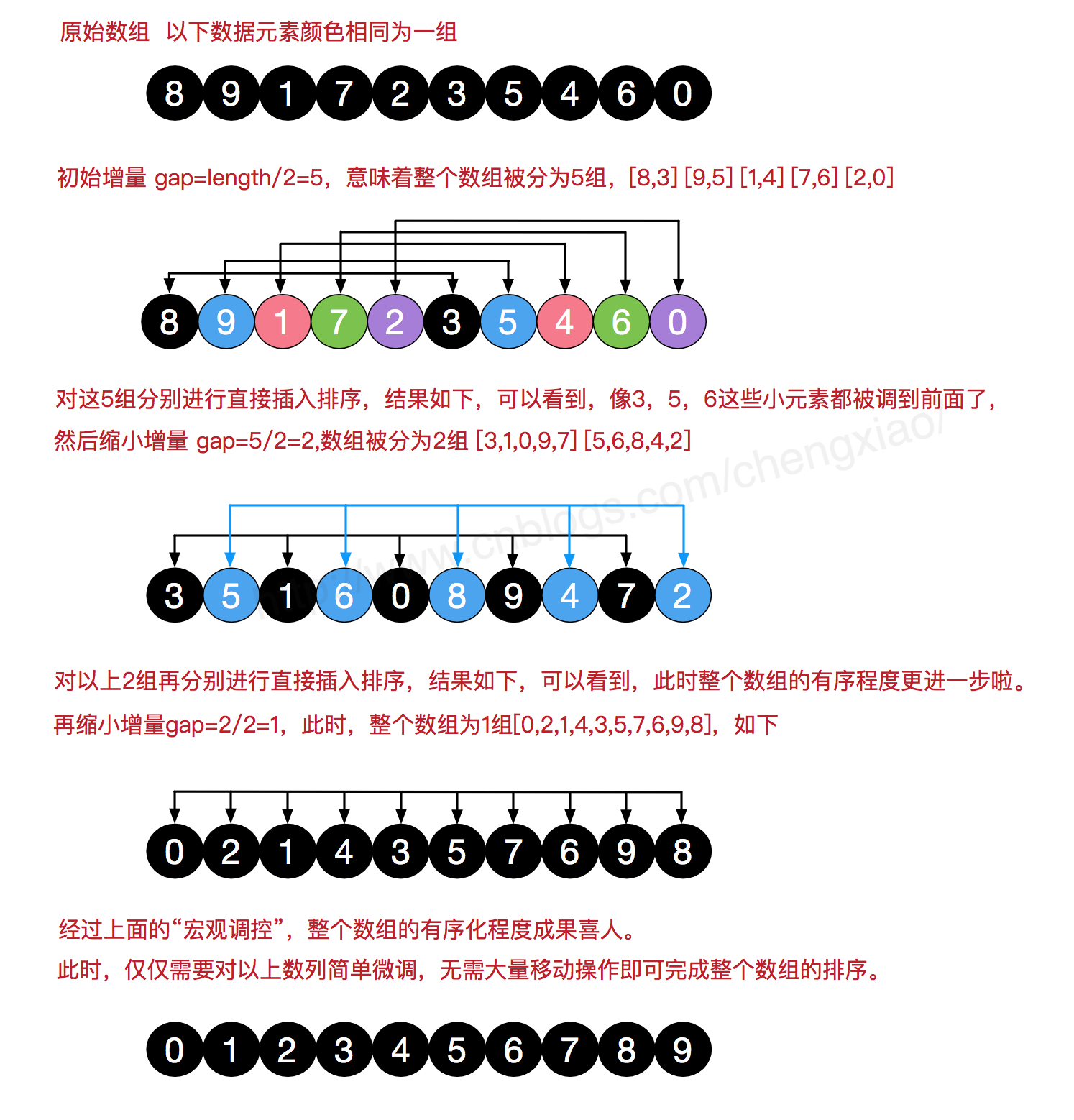
升序希尔算法描述如下:
1、选择增量gap=length/2,把元素分成gap组,每组取值为{i,i+gap,i+2gap,…}。
2、分别对每一组中的数据进行从前到后扫描插入排序。
3、缩小增量gap = gap/2,这种增量选择可以用一个序列来表示,{n/2,(n/2)/2…1},称为增量序列。
4、重复步骤2~3,直到增量gap=1。
1 | // 希尔排序 |
7. 简单选择排序
选择排序是一种简单直观的排序算法。它的工作原理很容易理解:初始时在序列中找到最小(大)元素,放到序列的起始位置作为已排序序列;然后,再从剩余未排序元素中继续寻找最小(大)元素,放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
注意选择排序与冒泡排序的区别:冒泡排序通过依次交换相邻两个顺序不合法的元素位置,从而将当前最小(大)元素放到合适的位置;而选择排序每遍历一次都记住了当前最小(大)元素的位置,最后仅需一次交换操作即可将其放到合适的位置。
升序简单选择排序描述如下:
1、未排序序列中,假设最小元素指针position指向第一个元素i。
2、依次对比所有未排序元素,遇到更小的元素,则把position指向更小的元素。
3、遍历未排序序列结束,交换position和i的元素,i位置排序完成。
4、重复1到3,直到所有位置排序完成。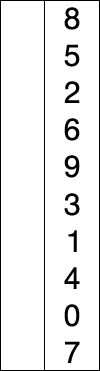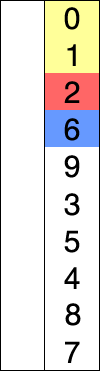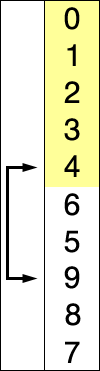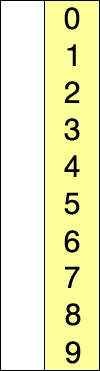
1 | // 简单选择排序 |
8. 堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏、最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
堆排序的基本思想是:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
参照图解排序算法(三)之堆排序,升序堆排序描述如下:
1、构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
2、从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点arr.length/2-1),从右至左,从下至上进行调整。
3、交换位置后也许子根结构混乱,那么继续调整,直到构造完成大顶堆。
4、将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,构造成大顶堆。再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
1 | // 堆排序 |
9. 归并排序
归并排序是创建在归并操作上的一种有效的排序算法,效率为O(nlogn),1945年由冯·诺伊曼首次提出。
归并排序的实现分为递归实现与非递归(迭代)实现。递归实现的归并排序是算法设计中分治策略的典型应用,我们将一个大问题分割成小问题分别解决,然后用所有小问题的答案来解决整个大问题。非递归(迭代)实现的归并排序首先进行是两两归并,然后四四归并,然后是八八归并,一直下去直到归并了整个数组。
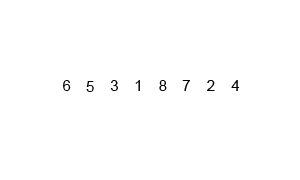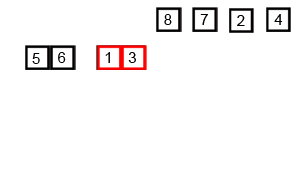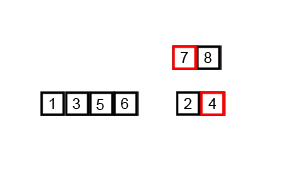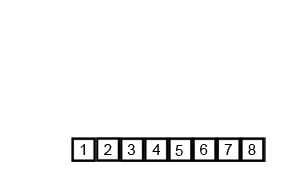
归并排序算法主要依赖归并(Merge)操作。归并操作指的是将两个已经排序的序列合并成一个序列的操作,归并操作步骤如下:
1、申请空间,该空间用来存放合并后的序列
2、设定两个指针,最初位置分别为两个已经排序序列的起始位置
3、比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
4、重复步骤3直到某一指针到达序列尾
5、将另一序列剩下的所有元素直接复制到合并序列尾
参照图解排序算法(四)之归并排序,代码如下:
1 | // 归并排序 |
10. 基数排序
基数排序的发明可以追溯到1887年赫尔曼·何乐礼在打孔卡片制表机上的贡献。它是这样实现的:将所有待比较正整数统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始进行基数为10的计数排序,一直到最高位计数排序完后,数列就变成一个有序序列(利用了计数排序的稳定性)。
基数排序步骤如下:
1、初始化:构造一个10*n的二维数组,一个长度为n的数组用于存储每次位排序时每个桶子里有多少个元素。
2、循环操作:从低位开始(我们采用LSD的方式),将所有元素对应该位的数字存到相应的桶子里去(对应二维数组的那一列)。然后将所有桶子里的元素按照桶子标号从小到大取出,对于同一个桶子里的元素,先放进去的先取出,后放进去的后取出(保证排序稳定性)。这样原数组就按该位排序完毕了,继续下一位操作,直到最高位排序完成。
参考基数排序详解以及java实现,代码如下:
1 | // 基数排序 |
11. 源码地址
https://github.com/voidking/leetcode/tree/master/src/com/voidking/leetcode/sort